https://www.acmicpc.net/problem/17070
17070번: 파이프 옮기기 1
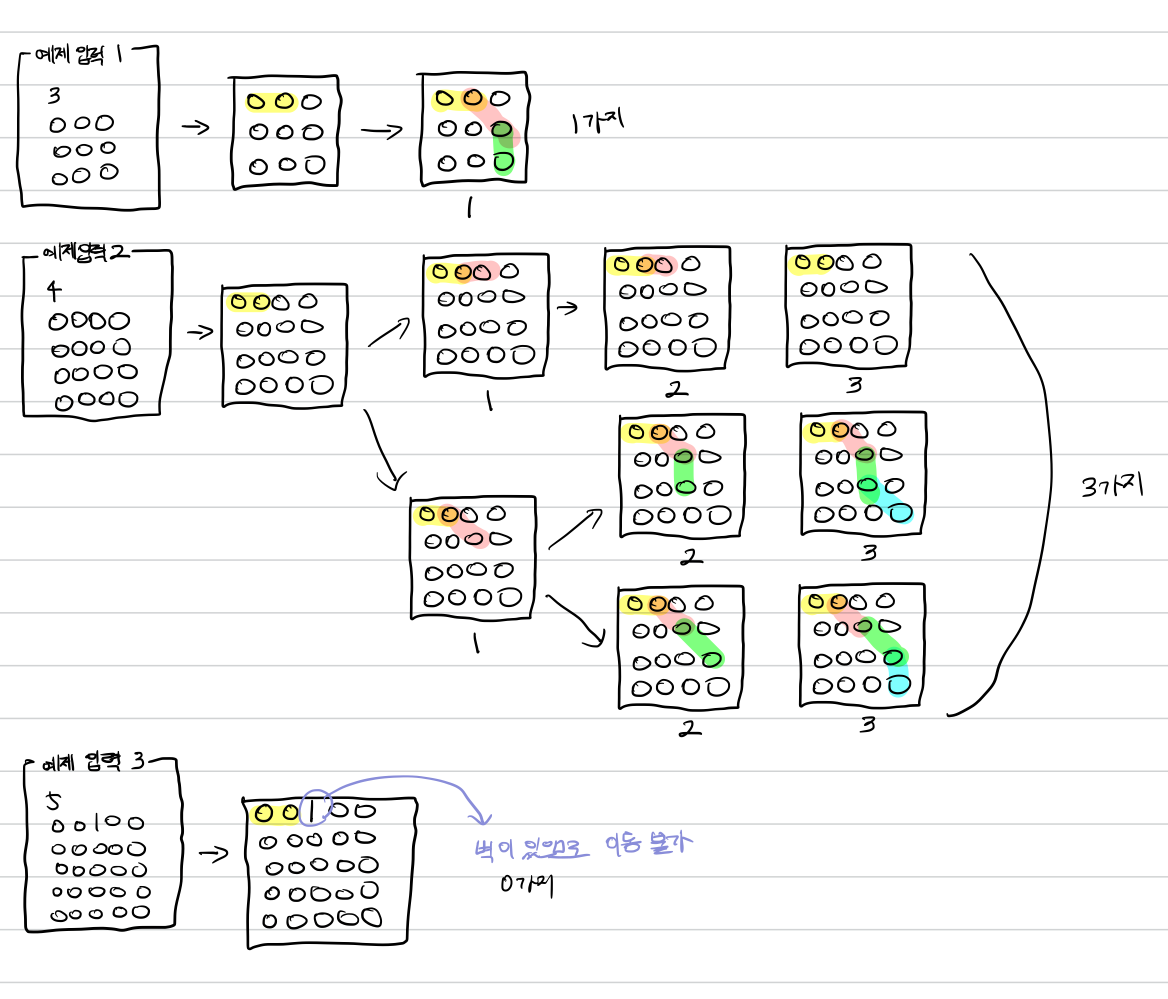
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net


import sys
input = sys.stdin.readline # 입력을 빠르게 받기 위해 sys.stdin.readline 사용
n = int(input()) # 격자의 크기 입력 받기
map = [list(map(int, input().split())) for _ in range(n)] # 격자 정보 입력 받기
dp = [[[0, 0, 0] for _ in range(n)] for _ in range(n)] # dp[i][j][k]: (i, j) 위치에서 k 방향으로 놓인 파이프의 경우의 수
# 파이프의 방향 설정: dp[가로][대각선][세로]
dp[0][1][0] = 1 # 첫 시작점이 [0,0]에서 가로방형인 [0,1]에서 시작하므로 dp를 dp[0][1][0] = 1로 초기화 해준다.
for i in range(n): # 동적 계획법(DP)을 이용하여 경우의 수 계산
for j in range(2, n):
if map[i][j] == 0: # 현재 위치가 벽이 아니라면
if i >= 1: # 세로 방향으로 이동할 수 있는 경우의 수 계산
dp[i][j][1] += dp[i - 1][j][1] + dp[i - 1][j][2]
if map[i - 1][j] == 0 and map[i][j - 1] == 0: # 대각선 방향으로 이동할 수 있는 경우의 수 계산
dp[i][j][2] += sum(dp[i - 1][j - 1])
dp[i][j][0] += dp[i][j - 1][0] + dp[i][j - 1][2] # 가로 방향으로 이동할 수 있는 경우의 수 계산
print(sum(dp[-1][-1])) # 목적지에서 가로, 대각선, 세로 방향으로 놓인 파이프의 경우의 수 합산
"""# 각 단계별로 dp 배열 출력
for i in range(n):
for j in range(n):
print(dp[i][j], end=" ")
print()
"""'백준 : 동적 프로그래밍' 카테고리의 다른 글
| 백준 : 1로 만들기(1463) with 자바 (0) | 2023.10.08 |
|---|---|
| 백준 : 피보나치 함수(1003) with 자바 (0) | 2023.10.08 |
| 백준 : 가장 긴 바이토닉 부분 수열(11054) with 자바 (0) | 2023.09.24 |
| 백준 : 제곱수들의 합(1699) with 자바 (0) | 2023.09.24 |
| 백준 : LCS(9251) with 파이썬 (0) | 2023.08.18 |
https://www.acmicpc.net/problem/17070
17070번: 파이프 옮기기 1
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net



import sys
input = sys.stdin.readline # 입력을 빠르게 받기 위해 sys.stdin.readline 사용
n = int(input()) # 격자의 크기 입력 받기
map = [list(map(int, input().split())) for _ in range(n)] # 격자 정보 입력 받기
dp = [[[0, 0, 0] for _ in range(n)] for _ in range(n)] # dp[i][j][k]: (i, j) 위치에서 k 방향으로 놓인 파이프의 경우의 수
# 파이프의 방향 설정: dp[가로][대각선][세로]
dp[0][1][0] = 1 # 첫 시작점이 [0,0]에서 가로방형인 [0,1]에서 시작하므로 dp를 dp[0][1][0] = 1로 초기화 해준다.
for i in range(n): # 동적 계획법(DP)을 이용하여 경우의 수 계산
for j in range(2, n):
if map[i][j] == 0: # 현재 위치가 벽이 아니라면
if i >= 1: # 세로 방향으로 이동할 수 있는 경우의 수 계산
dp[i][j][1] += dp[i - 1][j][1] + dp[i - 1][j][2]
if map[i - 1][j] == 0 and map[i][j - 1] == 0: # 대각선 방향으로 이동할 수 있는 경우의 수 계산
dp[i][j][2] += sum(dp[i - 1][j - 1])
dp[i][j][0] += dp[i][j - 1][0] + dp[i][j - 1][2] # 가로 방향으로 이동할 수 있는 경우의 수 계산
print(sum(dp[-1][-1])) # 목적지에서 가로, 대각선, 세로 방향으로 놓인 파이프의 경우의 수 합산
"""# 각 단계별로 dp 배열 출력
for i in range(n):
for j in range(n):
print(dp[i][j], end=" ")
print()
"""'백준 : 동적 프로그래밍' 카테고리의 다른 글
| 백준 : 1로 만들기(1463) with 자바 (0) | 2023.10.08 |
|---|---|
| 백준 : 피보나치 함수(1003) with 자바 (0) | 2023.10.08 |
| 백준 : 가장 긴 바이토닉 부분 수열(11054) with 자바 (0) | 2023.09.24 |
| 백준 : 제곱수들의 합(1699) with 자바 (0) | 2023.09.24 |
| 백준 : LCS(9251) with 파이썬 (0) | 2023.08.18 |
