알고리즘 3주차( 분할 정복)
분할 정복 설계
분할정복은 크게 3가지로 설계할 수 있다.
2.정복(Conquer) 단계
3.합병(Merge) 단계

최댓값과 최솟값 찾기

문제: 크기가 n인 배열내의 요소들 중 최댓값과 최솟값을 찾는다.
쉬운 전략
총 비교 횟수 = (n – 1) + (n – 2) = 2n - 3






자연어 알고리즘 :
1. 크기가 (high + 1)인 배열 ㅠ


비재귀 합병 정렬
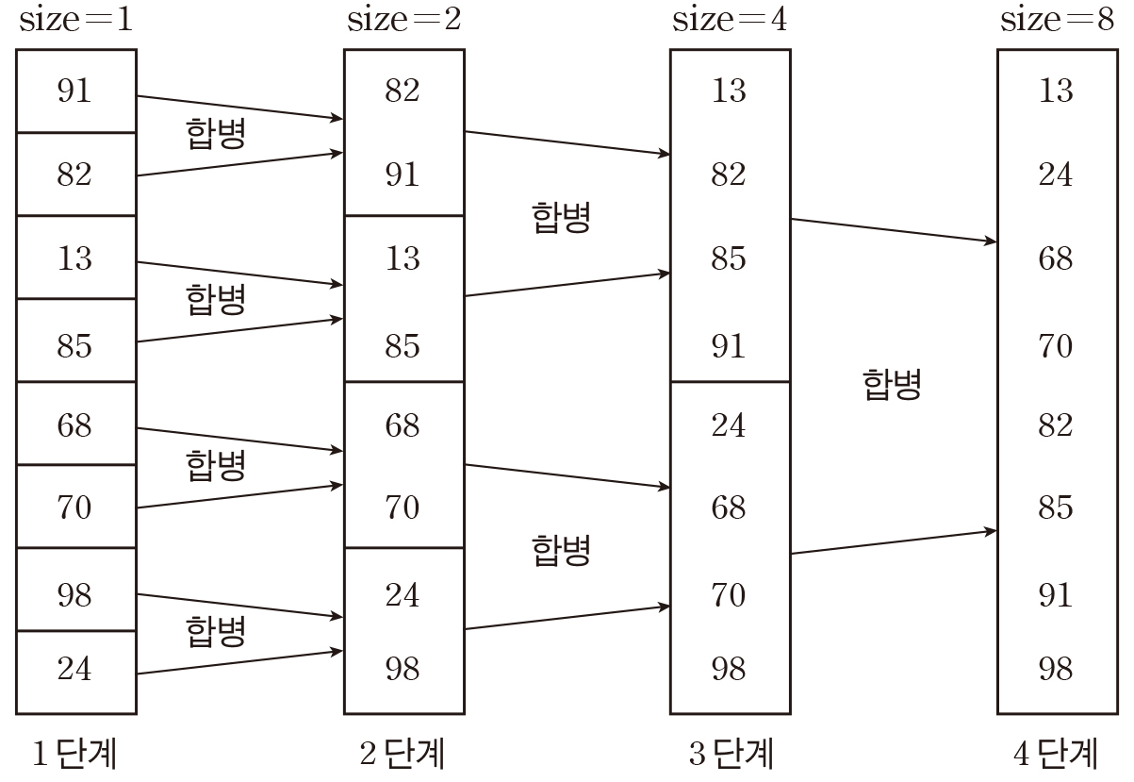
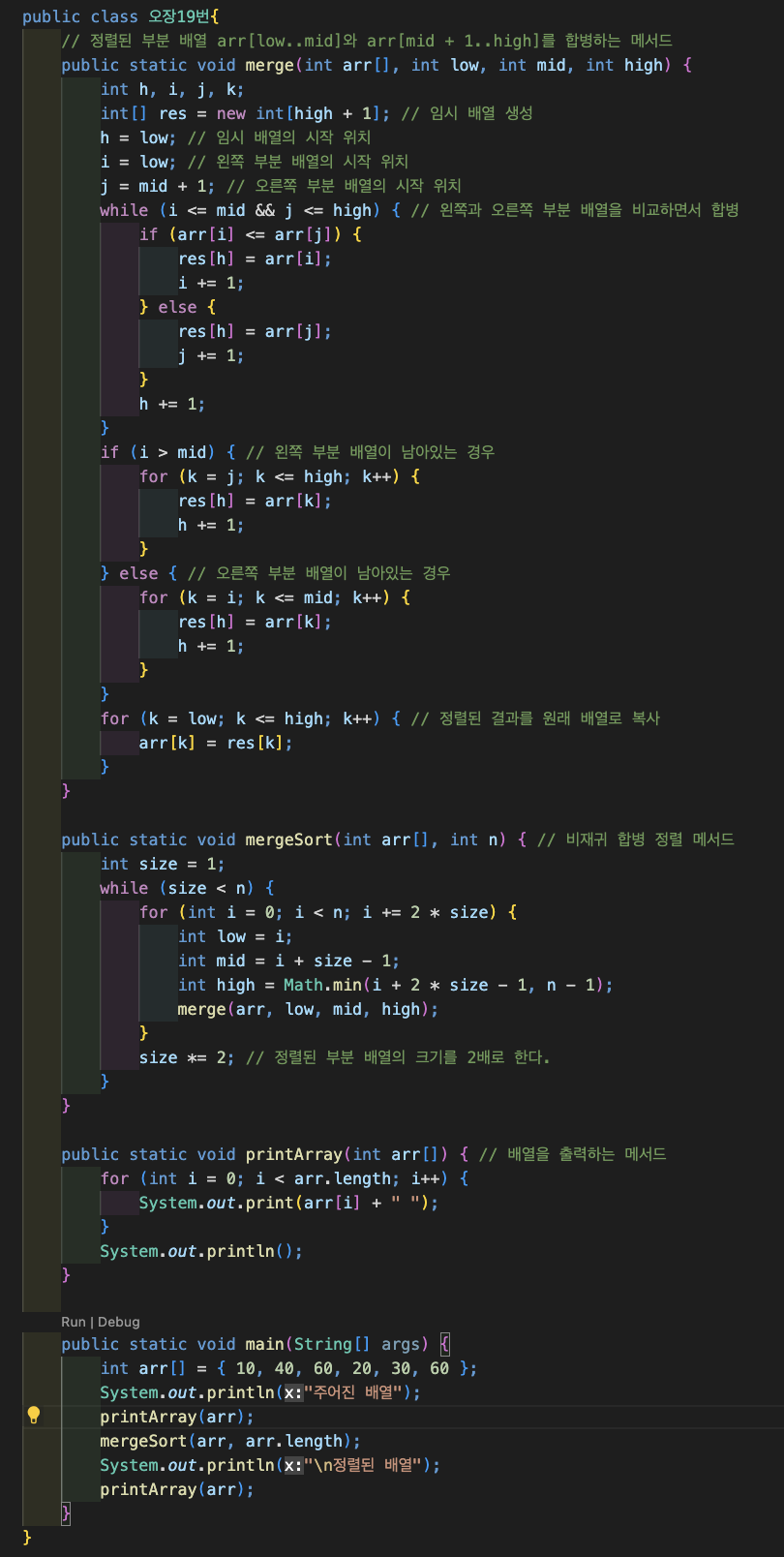

합병 정렬의 단점
- 합병 정렬의 공간 복잡도: O(n)
- 입력을 위한 메모리 공간 (입력 배열)외에 추가로 입력과 같은 크기의 공간 (임시 배열)이 별도로 필요하다.
- 2개의 정렬된 부분을 하나로 합병하기 위해 합병된 결과를 저장할 공간이 필요하기 때문이다.
합병정렬의 응용
- 합병정렬은 외부정렬의 기본이 되는 정렬 알고리즘이다.
- 그렇기 때문에 연결 목록에 있는 데이터를 정렬할 때 빠른 정렬이나 힙 정렬 보다 효율적이다.
- 멀티코어 CPU와 다수의 프로세서로 구성된 그래픽 처리 장치의 등장으로 정렬 알고리즘을 병렬화하기 위해 합병 정렬 알고리즘이 활용된다.
빠른 정렬
- 가장 빠른 정렬 알고리즘은 아니지만 평균적으로 효율적이다.
- 평균 시간 복잡도 : θ(nlogn)
- 최악 시간 복잡도 : θ(n^2)


최초 호출: quickSort(A, 0, n - 1)
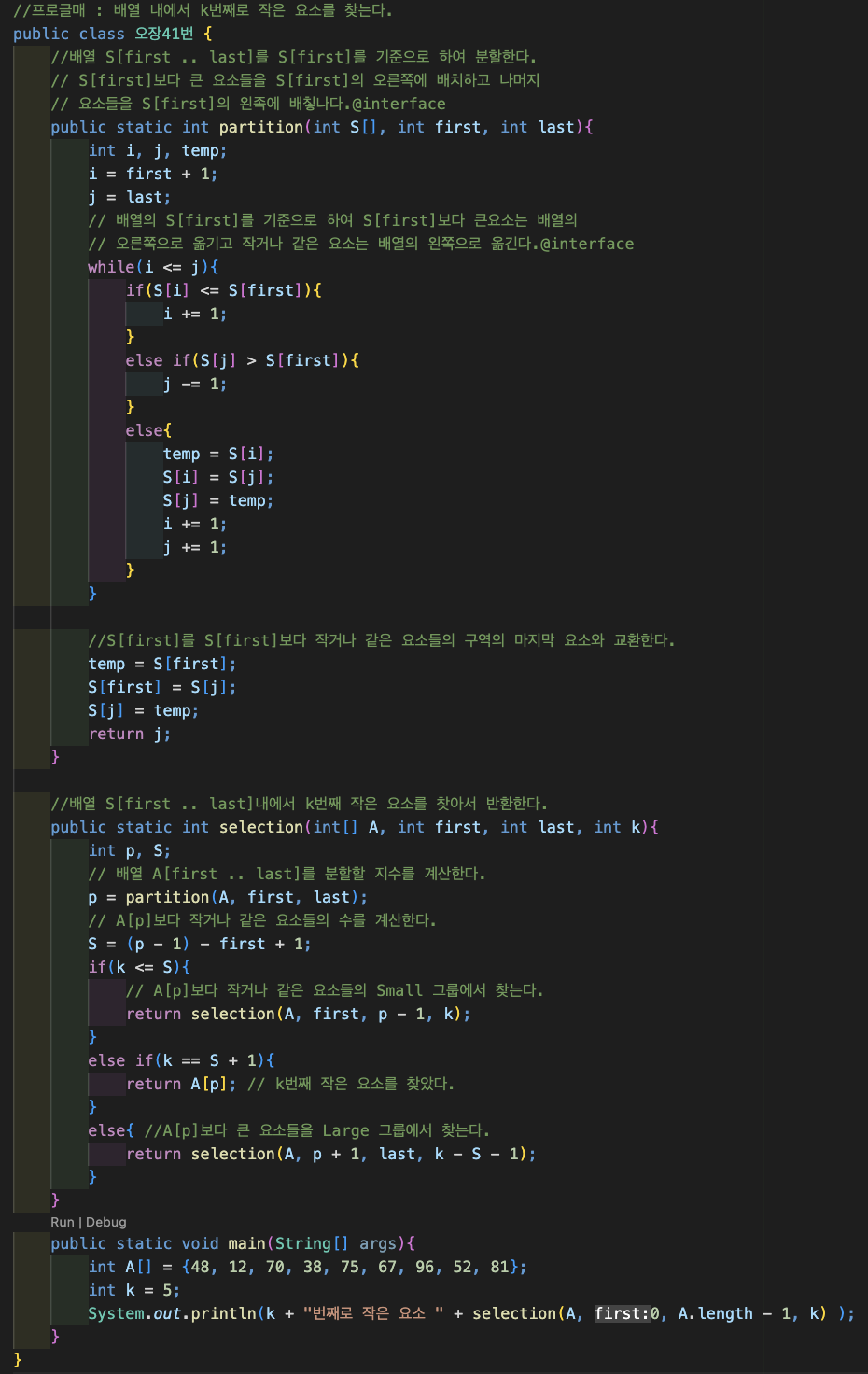
선택 알고리즘



경우 1: Small 그룹의 크기 ≥ k
k번째로 작은 숫자를 Small 그룹에서 찾는다.
경우 2: Small 그룹의 크기 < k
k번째로 작은 숫자를 Large 그룹에서 찾는다.
이 경우 Large 그룹에서 (k – s - 1)번째로 작은
숫자를 찾아야 한다. 여기서 s는 Small 그룹에
있는 숫자들의 수이다.


분할 정복이 부적절한 경우
- 문제가 분할될 때마다 분할된 부분 문제들의 입력 크기의 합이 분할되기 전의 입력 크기보다 매우 커지는 경우
경우 1: 크기 n인 문제가 거의 n에 가까운 크기의 2개 이상의 부분 문제들로 분할
경우 2: 크기 n인 문제가 n/c 크기의 거의 n개의 부분 문제 들로 분할. c는 상수

